FPMC¶
Introduction¶
Title: Factorizing personalized Markov chains for next-basket recommendation
Authors: Steffen Rendle, Christoph Freudenthaler, Lars Schmidt-Thieme
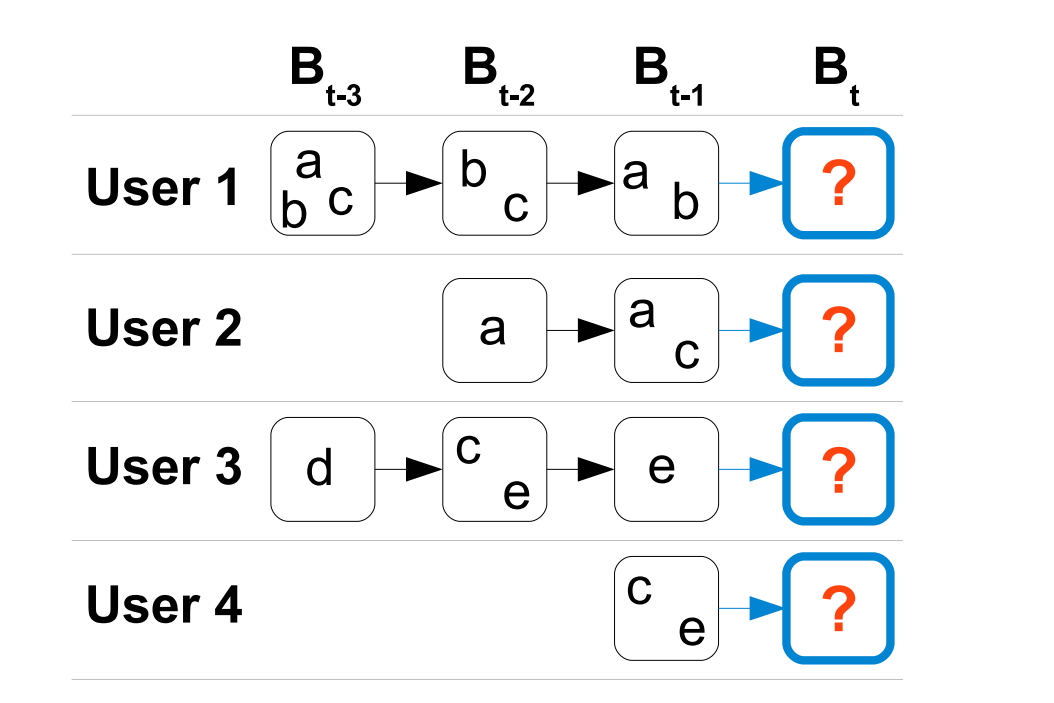
Abstract: Recommender systems are an important component of many websites. Two of the most popular approaches are based on matrix factorization (MF) and Markov chains (MC). MF methods learn the general taste of a user by factorizing the matrix over observed user-item preferences. On the other hand, MC methods model sequential behavior by learning a transition graph over items that is used to predict the next action based on the recent actions of a user. In this paper, we present a method bringing both approaches together. Our method is based on personalized transition graphs over underlying Markov chains. That means for each user an own transition matrix is learned – thus in total the method uses a transition cube. As the observations for estimating the transitions are usually very limited, our method factorizes the transition cube with a pairwise interaction model which is a special case of the Tucker Decomposition. We show that our factorized personalized MC (FPMC) model subsumes both a common Markov chain and the normal matrix factorization model. For learning the model parameters, we introduce an adaption of the Bayesian Personalized Ranking (BPR) framework for sequential basket data. Empirically, we show that our FPMC model outperforms both the common matrix factorization and the unpersonalized MC model both learned with and without factorization.
Running with RecBole¶
Model Hyper-Parameters:
embedding_size (int): The embedding size of users and items. Defaults to64.loss_type (str): The type of loss function. It is set to'BPR', the training task will be optimized in the pair-wise way, which maximizes the difference between the positive item and the negative one. In this way, negative sampling is necessary, such as setting--train_neg_sample_args="{'distribution': 'uniform', 'sample_num': 1}". Defaults to'BPR'. Range in['BPR'].
A Running Example:
Write the following code to a python file, such as run.py
from recbole.quick_start import run_recbole
parameter_dict = {
'train_neg_sample_args': None,
}
run_recbole(model='FPMC', dataset='ml-100k', config_dict=parameter_dict)
And then:
python run.py
Notes:
Different from other sequential models, FPMC must be optimized in pair-wise way using negative sampling, so it needs
train_neg_sample_args="{'distribution': 'uniform', 'sample_num': 1}".
Tuning Hyper Parameters¶
If you want to use HyperTuning to tune hyper parameters of this model, you can copy the following settings and name it as hyper.test.
learning_rate choice [0.01,0.005,0.001,0.0005,0.0001]
Note that we just provide these hyper parameter ranges for reference only, and we can not guarantee that they are the optimal range of this model.
Then, with the source code of RecBole (you can download it from GitHub), you can run the run_hyper.py to tuning:
python run_hyper.py --model=[model_name] --dataset=[dataset_name] --config_files=[config_files_path] --params_file=hyper.test
For more details about Parameter Tuning, refer to Parameter Tuning.
If you want to change parameters, dataset or evaluation settings, take a look at